Compito CL - Seconda Prova

Si consideri la seguente frase:

Non è possibile che, se Socrate è un uomo e gli uomini sono mortali, allora Socrate sia immortale.

Immaginando di utilizzare le seguenti lettere proposizionali:

• SU = SocrateUomo, vera se Socrate è un uomo
• UM = UominiMortali, vera se tutti gli uomini sono mortali
• SM = SocrateMortale, vera se Socrate è mortale

indicare quele delle seguenti sono formalizzazioni corrette:

• ¬ ⋄ (SU ∧ UM ⊃ ¬ SM)
• □ ¬ (SU ∧ UM ⊃ ¬ SM)
• □ (SU ∧ UM ∧ SM)
• ¬ ⋄ (SU ∧ UM) ⊃ ¬ ⋄ (¬ SM)
• □ (SU ∧ UM) ⊃ ⋄ (¬ SM)
• ¬ (⋄ (SU ∧ UM)) ⊃ ⋄ (¬ SM)

Si consideri il seguente frame

\[F = < W, R >\]

dove:

• W = N, l’insieme dei numeri naturali
• R = { (i,i+1) | i ∈ N and i >= 1 }

Si consideri una formula atomica \(\phi\) per cui vale la seguente proprietà:

Dire quali delle seguenti affermazioni sono vere:

• F ⊨ ϕ ⊃ □ ¬ ϕ
• F ⊨ ¬ ϕ ⊃ □ ϕ
• F ⊨ □ (¬ ϕ ⊃ ⋄ ϕ)
• F ⊨ □ □ ϕ
• F ⊨ ϕ ∧ □ ¬ ϕ
• F ⊨ ¬ (□ ϕ ∨ ¬ □ ϕ)

Una formula A è valida

• in un mondo w, se e solo se M , w ⊨ A per ogni I , con w ∈ W, F = <W, R> e M = <F,I>
• nella classe dei frame seriali C, se e solo se F ⊨ A per ogni F = <W, R> e, per ogni w ∈ W, esiste w ′ tale che R(w, w′)
• nella classe dei frame riflessivi C, se A è nella forma B ⊃ ⋄ B
• nella classe dei frame simmetrici C, se A è nella forma B ⊃ □ ¬ □ ¬ B

Sia dato il frame F come nella seguente figura, in cui ogni nodo rappresenta un mondo, gli archi relazioni di accessibilità tra mondi e, in ogni mondo, ad esempio w1, viene riportato l’elenco delle formule vere nel mondo, ad es, A, B:

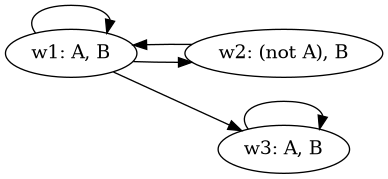
La formula C= ⋄ □ (A ∧ B) è tale per cui:

• w2 ⊨ ¬ C
• w3 ⊨ C
• F ⊨ ¬ ¬ C
• w1 ⊨ ¬ C

[Suggerimento: testate la soddisfacibilità di C nei tre casi (w1, w2, w3), un mondo alla volta, verificando ogni volta se C è vera in quel mondo.]

Usando il metodo del Tableau, dire se la seguente formula è valida, soddisfacibile, insoddisfacibile.

• Soddisfacibile
• Valida
• Insoddisfacibile

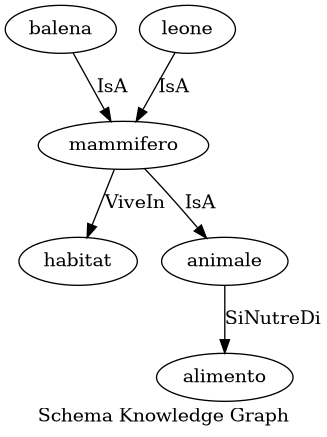
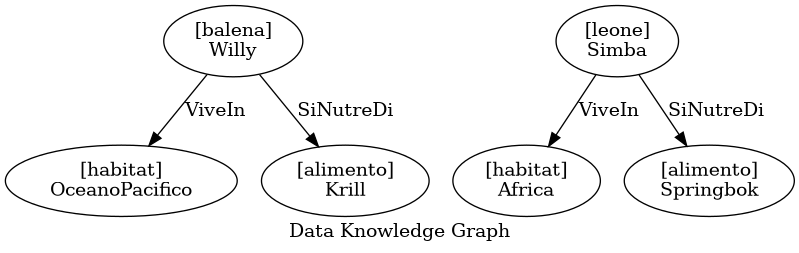
Quale o quali delle seguenti formalizzazioni in DL sono compatibili con lo Schema Knowledge Graph (SKG) ed il Data Knowledge Graph (DKG) dati in figura?

Si noti che nel Data Knowledge Graph, il testo tra parentesi quadre indica la classe dell’istanza. Ad esempio “[balena] Willy” significa che Willy è una balena.

• TBOX = {
     balena ⊑ mammifero
     mammifero ⊑ animale
     […]
  }
  ABOX = {
     balena(Willy)
     vive_in(Willy, OceanoPacifico)
     […]
  }
  

• TBOX = {
    balena ⊑ mammifero ⊓ leone
    mammifero ⊑ animale
    […]
  }
  ABOX = {
    balena(Willy)
    […]
  }
  

• TBOX = {
     balena ⊑ mammifero
     mammifero ⊑ animale
     vive_in(Simba, Africa)
     […]
  }
  ABOX = {
    balena(Willy)
    vive_in(Willy, OceanoPacifico)
    […]
  }
  

• TBOX = {
    mammifero ⊑ balena ⊔ leone
    mammifero ⊑ animale
    […]
  }
  ABOX = {
    balena(Willy)
    […]
  }
  

Dati lo Schema Knowledge Graph (SKG) e il Data Knowledge Graph (DKG) in figura, quali delle seguenti affermazioni sono vere?

(Ricordiamo che si dice che una teoria è consistente se e solo se è soddisfacibile.)

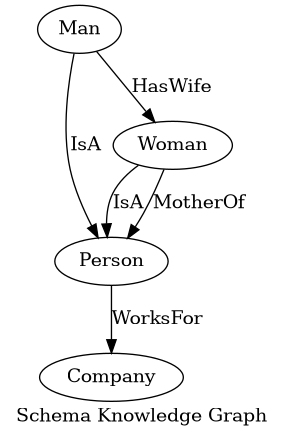
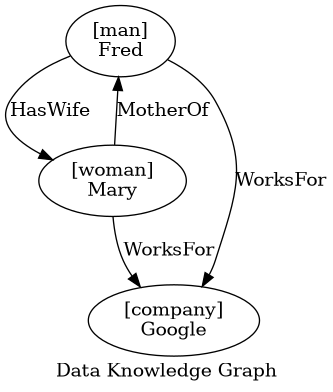
• Il Data Knowledge Graph è consistente con lo Schema Knowledge Graph
• Se uno aggiunge nella TBOX l’assioma Disjoint(Man, Woman), il DKG è consistente con lo SKG
• Se uno aggiunge nella ABOX l’asserzione ¬MotherOf(Mary,Fred) il DKG è consistente con lo SKG
• Se uno aggiunge nella ABOX l’asserzione ¬MotherOf(Mary,Fred) il DKG è consistente
• Il Data Knowledge Graph non è consistente

Data una TBOX T e due formule P, Q, quali delle seguenti affermazioni sono vere?

• P e Q sono soddisfacibili rispetto a T sse T ⊨ P ∧ Q
• Disjointness (P,Q) implica ¬ ( P ⊑ Q )
• Disjointness (P,Q) implica ¬ (Q ⊑ P ⊔ P ⊑ Q)
• ( P ⊑ Q) implica Disjointness (P, Q)
• Disjointness (P,Q) implica P ⊑ Q
• Disjointness (P,Q) se e solo se ¬ ( Q ⊑ P ⊔ P ⊑ Q)

Di seguito scriviamo CWA per significare Closed World Assumption and OWA per significare Open World Assumption. Si considerino la seguente TBOX ed ABOX:

Dire quali delle seguenti affermazioni sono vere:

• B(u1) può essere dedotto seguendo la regola della OWA applicata alla ABOX
• ogni formula derivabile applicando la OWA può essere derivata applicando anche la CWA
• not B(u2) (attenzione: u2!) può essere dedotto seguendo la regola della CWA applicata alla ABOX
• ogni formula derivabile applicando la CWA può essere derivata applicando anche la OWA
• not B(u1) può essere dedotto seguendo la regola dell OWA applicata alla ABOX

Data la seguente teoria:

TBOX = {
  A ≡ B ⊓ C
  C ≡ D ⊓ E
  E \(\sqsubseteq\) F ⊓ G
}
ABOX {
  A(1)
}

Espandere ABOX nella TBOX, ricordando che l’espansione contiene esclusivamente concetti primitivi e decidere quali di queste affermazioni sono vere.

B(1)
D(1)
F(1)
G(1)

A(1)
C(1)
E(1)

B(1)
D(1)
F(1) ⊔ G(1)

B(1) ⊓ C(1)
D(1) ⊓ E(1)
F(1) ⊓ G(1)