June 2021

Il gatto di Schrödinger è un famoso esperimento del pensiero della fisica quantistica, che semplifichiamo nel seguente modo:

“un gatto è chiuso in una scatola con una fiala avvelenata, che può rilasciare il suo veleno in un momento casuale, uccidendo il gatto. Se la scatola è chiusa, non sappiamo dire se il gatto è vivo o morto. Se però la scatola è aperta, siamo in grado di dire se il gatto è vivo o morto”.

Immaginando di usare i seguenti simboli proposizionali:

• CAT_IN_BOX: vera se il gatto è nella scatola
• BOX_OPEN: vera se la scatola aperta, falsa se la scatola è chiusa
• CAT_ALIVE: vera se il gatto è vivo, falsa se il gatto è morto
• POISON_RELEASED: vera se il veleno è stato rilasciato, falsa se il veleno non è stato ancora rilasciato

Dire quali di queste formule sono vere in una teoria che formalizza in Logica Proposizionale il dominio di cui sopra.

• [SI] CAT_IN_BOX
• [SI] not BOX_OPEN imp (CAT_ALIVE or not CAT_ALIVE)
• CAT_ALIVE imp POISON_RELEASED
• [SI] BOX_OPEN imp (CAT_ALIVE or not CAT_ALIVE)
• [SI] POISON_RELEASED imp (not CAT_ALIVE)
• BOX_OPEN

Date le formule:

• \(\alpha\): \((\neg A \vee \neg B\)\)
• \(\beta\): \((A \vee B \vee \neg B) \wedge \neg (A \wedge B)\)
• \(\gamma\): \(A \supset B\)

Usare le tabelle della verità per verificare quali delle seguenti affermazioni sono vere.

• [SI] \(\alpha\) è equivalente a \(\beta\)
• \(\gamma\) è conseguenza logica di \(\beta\)
• [SI] \(\beta \longleftrightarrow \gamma\) è soddisfacibile, dove \(\longleftrightarrow\) è il connettivo logico per “se e solo se”

Dire quale delle seguenti formule è sicuramente soddisfacibile

• not A, dove A è soddisfacibile
• [SI] A
• not A, dove A è valida
• [SI] A or not A
• [SI] not (A and not A)
• [SI] not A, dove A è insoddisfacibile

Indicare quale delle seguenti formule formalizza la seguente frase:

“Ogni persona ha un documento di identità in cui compaiono la foto e il nome della persona a cui il documento fa riferimento.”

• \(\forall x. (Persona(x) \,\wedge\, \exists y. (Ha(x, y) \,\wedge\, Contiene(y, foto(x)) \,\wedge\, Contiene(y, nome(x)))\)
• \(\forall x. \exists y. (Persona(x) \,\wedge\, Ha(x, y) \,\wedge\, Contiene(y, foto(x)) \,\wedge\, Contiene(y, nome(x)))\)
• [SI] \(\forall x. (Persona(x) \supset \exists y. (Ha(x, y) \,\wedge\, Contiene(y, foto(x)) \,\wedge\, Contiene(y, nome(x)))\)
• [SI] \(\forall x. (\neg Persona(x) \,\vee\, \exists y. (Ha(x, y) \,\wedge\, Contiene(y, foto(x)) \,\wedge\, Contiene(y, nome(x)))\)
• \(\forall x. (Persona(x) \supset \forall y. (Ha(x, y) \,\wedge\, Contiene(y, foto(x)) \,\wedge\, Contiene(y, nome(x)))\)
• \(\exists x. (Persona(x) \supset \forall y. (Ha(x, y) \,\wedge\, Contiene(y, foto(x)) \,\wedge\, Contiene(y, nome(x)))\)

Produrre la definizione delle formule ben formate della Logica del primo ordine (15 righe max)

Sia \(L = (c_1, c_2, ..., f_1, f_2, ..., P_1, P_2, ...)\) un linguaggio del primo ordine dove

• \(c_i\) sono costanti,
• \(f_i\) sono simboli funzionali e
• \(P_i\) sono simboli predicativi.

Sia \((D,I)\) una funzione di interpretazione di \(L\), ove \(D\) è il dominio di interpretazione e \(I\) è la funzione di interpretazione. Dire quale di queste affermazioni sono vere

• [SI] \(I(f_2(c_1,c_2))\) è un elemento di \(D\), dove \(f_2\) è una funzione binaria
• [SI] \(I(f_1(c_1))\) è un elemento di \(D\), dove \(f_1\) è una funzione unaria
• [SI] \(I(P_1)\) è un sottoinsieme di \(D\), dove \(P_1\) è un predicato unario
• [SI] \(I(x)[a]\) è un elemento di \(D\); dove \(x\) è una variabile ed “\(a\)” è un assignment
• \(I(P_2)\) è un sottoinsieme di \(D\), dove \(P_2\) è un predicato binario
• \(I(P_2(c_1, c_2))\) è un sottoinsieme di D, dove \(P_2\) è un predicato binario
• \(I(P_{11}(c_1) \wedge P_{12}(c2))\) è un sottoinsieme di \(D\), dove \(P_{11}\) e \(P_{12}\) sono predicati unari

Si consideri il seguente frame

• \(F = < W, R >\)

dove:

• \(W = \{ 1, 2, 3, 4, 5, 6, 7 \}\)
• \(R = \{ (1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7), (4, 1), (5, 1), (6, 1) (7, 1) \}\)

Sia data la seguente funzione di interpretazione

• \(I(A) = \{ 1, 3, 5, 7 \}\)
• \(I(B) = \{ 2, 4, 6 \}\)

Dire quali delle seguenti affermazioni sono vere.

• [SI] \(F \models A \supset \diamond (A \vee B)\)
• [SI] \(F \models (A \wedge \neg B) \vee (\neg A \wedge B)\)
• \(F \models \square A\)
• [SI] \(F \models A \supset (A \vee B)\)
• [SI] \(F \models \diamond B \vee \diamond \diamond B\)
• \(F \models \diamond A\)

Usando il metodo del Tableau, verificare se la seguente formula:

\(□(P → ◇Q) → ◇(¬ P ∨ ◇ Q)\)

è valida, soddisfacibile, insoddisfacibile in S5.

• [SI] Valida
• Soddisfacibile ma non valida
• Insoddisfacibile
• Nessuna di quelle sopra

Definire formalmente i 4 “reasoning services” di una ABOX in una Logical Descrittiva (max 20 righe)

Sia dato il Knowledge Graph in figura

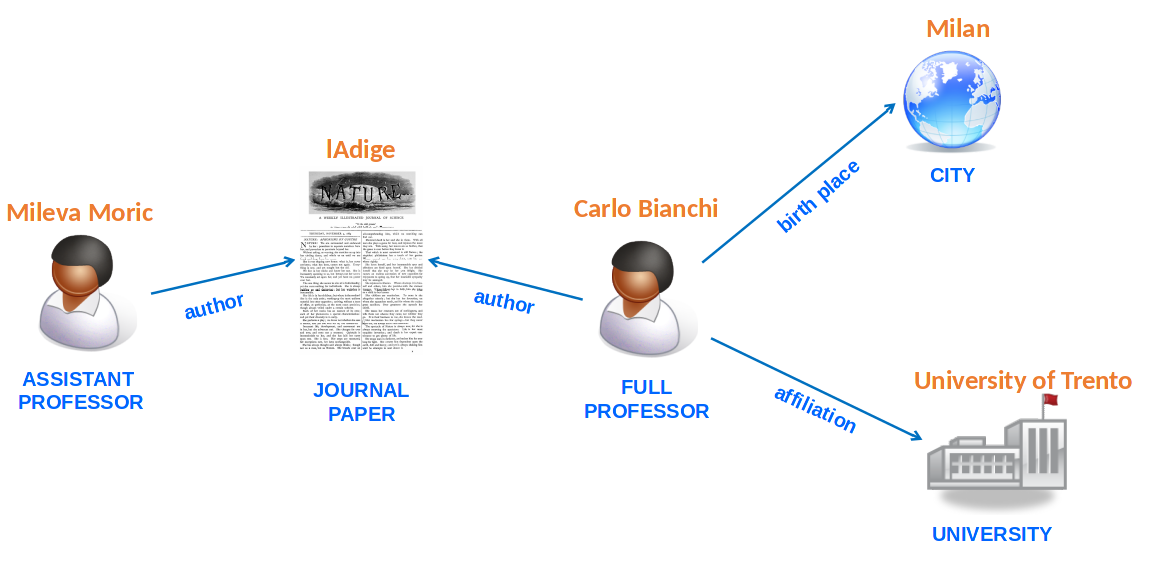
dove:

• i nomi sopra le figure sono i nomi delle istanze considerate
• i nomi sotto le figure rappresentano “role assertions” cioè il fatto che quelle istanze soddisfano quel concetto
• i link taggati rappresentano “role assertions” ossia il fatto che quella coppia di istanze soddisfano quel ruolo

Scrive la teoria, ossia l’insieme di assiomi che formalizza in Description Logic la conoscenza rappresentata nel knowledge graph.